Introduction to Pascal's Triangle

Pascal's Triangle plays a significant role in various natural sequences. By the end of this article, the enchantment surrounding it will be replaced with a clearer understanding.

The Binomial Theorem Explained

Where does this triangle originate? I won't delve deeply into its history, as it can be easily researched, and it isn't the primary focus of this piece. The intent here is to connect various mathematical concepts holistically. This triangle predates Blaise Pascal, having been recognized by several cultures.

The essence of Pascal's Triangle can be traced to the binomial theorem:

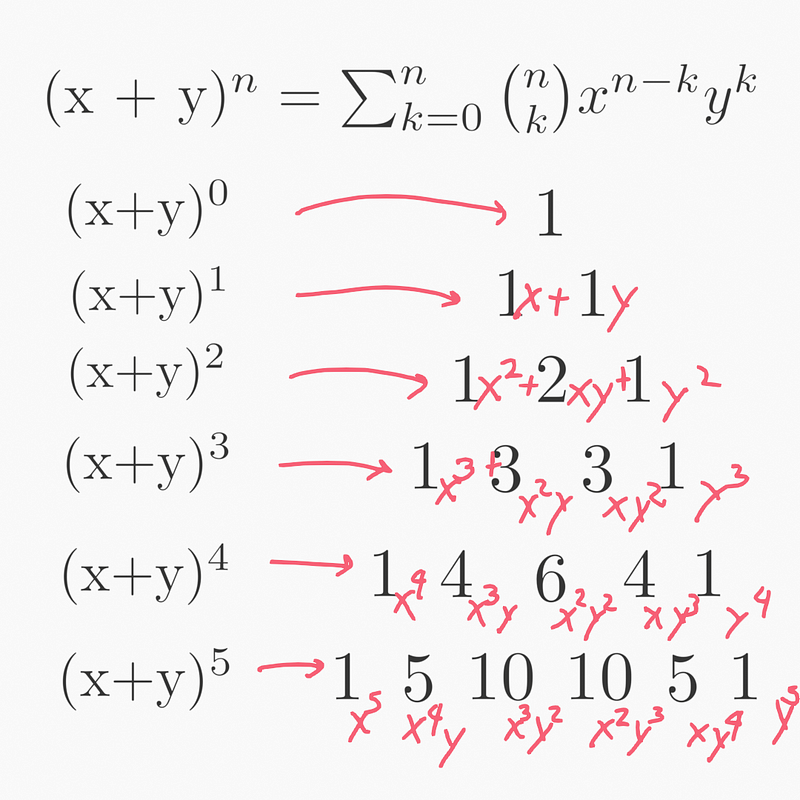
Thus, what we refer to as "Pascal's Triangle" is fundamentally rooted in the binomial theorem.

Understanding the Binomial Theorem

To grasp the binomial theorem, we explore convolutions—an essential concept. Essentially, it involves multiplying a binomial expression, such as (x + y), repeatedly. This multiplication is intrinsically linked to generating functions.

The multiplication of two polynomials can be viewed as a convolution of their coefficients, leading to the emergence of these patterns. While my interpretation emphasizes convolutions, most people typically rely on arithmetic to observe patterns and formulate a mathematical model.

The calculation of Pascal's Triangle involves adding the numbers directly above a given entry, which builds the triangle from top to bottom:

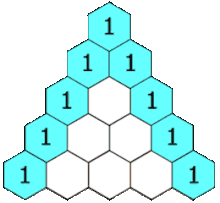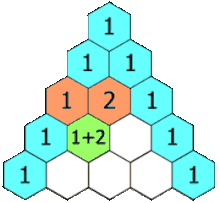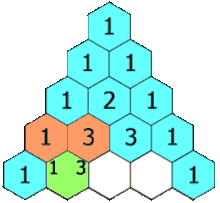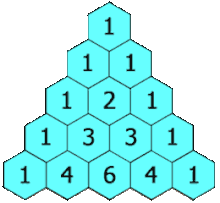
The Connection to Convolutions

This pattern doesn't arise by mere coincidence; it stems from the convolution properties of the binomial (x + y) multiplied repeatedly.

To illustrate this, consider a polynomial example of (x³ + 4x²y + 5xy² + 2y³) and its multiplication by (x + y). The convolution simplifies the process: simply add neighboring coefficients while shifting.

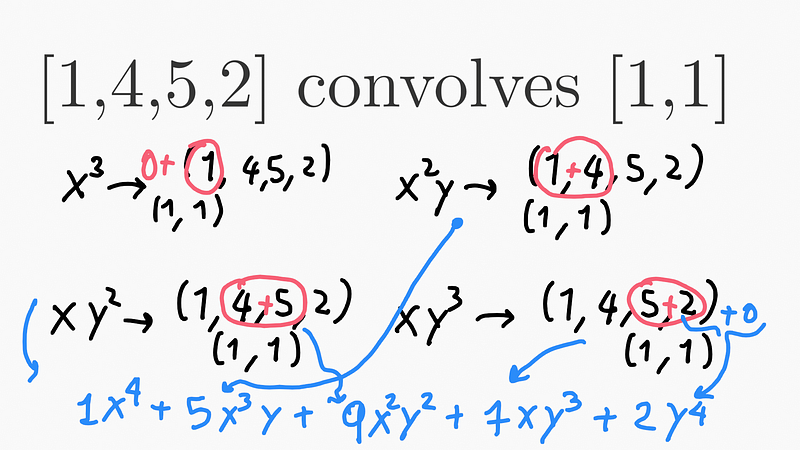
Thus, the rule of summing two numbers above in Pascal's Triangle is derived from the convolution behavior of (x + y). The beauty of interpreting polynomial multiplication through convolutions allows for a more straightforward understanding of many concepts.

Why Is This Pattern Common in Nature?

The mystical allure of Pascal's Triangle arises from its patterns aligning with various seemingly unrelated phenomena, all rooted in the binomial convolution behavior.

The Binomial Distribution

A significant aspect linking Pascal's Triangle to probability is the binomial distribution. The formula for this distribution mirrors that of the binomial theorem, substituting probabilities p and (1-p) for x and y, respectively, where p denotes the probability of a given event.

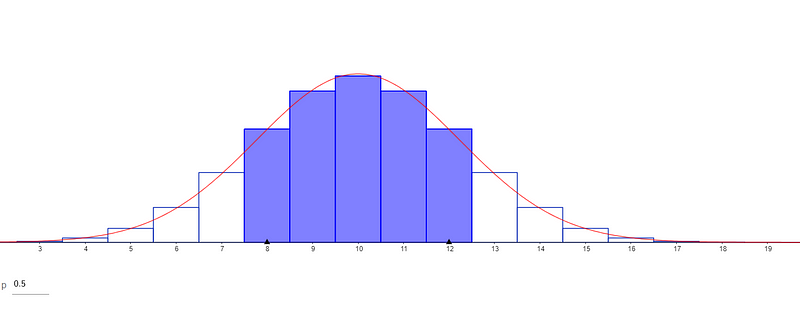
The Gaussian distribution, used widely for random variable description, also originates from the binomial theorem, emphasizing the importance of infinity in this context.

Fibonacci Sequence Connections

How does Pascal's Triangle relate to the Fibonacci sequence? The rule governing Pascal's Triangle—adding two preceding numbers to derive a new one—is similar to the Fibonacci sequence's method of summing the last pair of numbers.

Exploring Further Mysteries

The connections between Pascal's Triangle and various mathematical concepts, such as its relationship with powers of 2, combinatorics, and more, reveal intricate patterns worthy of exploration.

The first video, "A Deep Explanation Of Pascal's Triangle," provides an in-depth analysis of the triangle's properties and applications.

The second video, "What is the secret of Pascal's triangle?" delves into the hidden connections and significance of the triangle in mathematics.

Conclusion

In summary, understanding Pascal's Triangle unveils a wealth of knowledge about mathematical principles and their applications across various fields. Thank you for taking the time to read this exploration. Consider sharing this article to spread the insights!