Chapter 1: The Provocative Question

Let's dive into the intriguing question posed in the title. This statement holds true only under a specific interpretation of the equality sign. Before we elaborate on that, it’s essential to frame the discussion appropriately.

Here’s a little-known fact that mathematicians rarely discuss: there exist methods for summing and multiplying infinite sets of numbers such that, while the outcome should logically be infinite, it possesses unique arithmetic traits that make it appear as if it is a finite number. Some physicists even assert that these infinities can actually be viewed as finite values.

It’s almost as if the concept of infinity is accompanied by two entities: the notion of infinity itself and a finite numerical representation, or residue, that is uniquely tied to the series’ growth. The fascinating aspect that keeps me pondering is that this phenomenon isn’t merely theoretical—it can be validated through experiments (more on that later).

About a decade ago, the internet was abuzz when two physicists claimed they had demonstrated that the sum of all positive integers (1 + 2 + 3 + 4 + …) equals -1/12. Indeed, this assertion is accurate if we interpret the term “infinite sum” in a specific mathematical context.

Now, let's explore how this concept serves as a gateway to even more captivating ideas. For instance, under similar interpretations, we can consider the infinite product of positive integers as a finite value.

In fact, we arrive at the astonishing conclusion that:

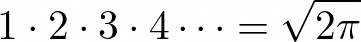
Using these methods, we can express divergent products over prime numbers, such as 2 × 3 × 5 × 7 × 11 × ... = 4². Before you dismiss this as nonsensical mathematical heresy, let me assure you that these techniques, despite their odd outcomes, are frequently employed in quantum field theory and string theory.

You might be wondering what’s happening here. Let’s delve deeper.

Oh, and if you’re reading this on a mobile device, you may need to switch to light mode to view the equations properly.

To derive these amusing results, we first need some background on a crucial concept: the Riemann zeta function.

Chapter 2: A Historical Perspective

In 1734, a then-unknown mathematician, Leonhard Euler, established that

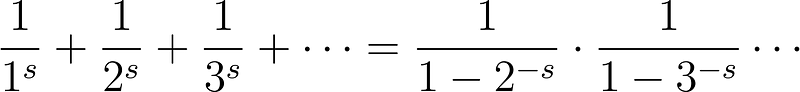
for any s > 1. The ellipsis at the end indicates continuation to infinity. On the left, we have the sum of natural numbers (1, 2, 3, …), and on the right, the product of prime numbers (2, 3, 5, 7, 11, …). Euler's discovery proved pivotal in understanding the distribution of prime numbers among the natural numbers.

We won’t shy away from notation, so let’s express this more compactly:

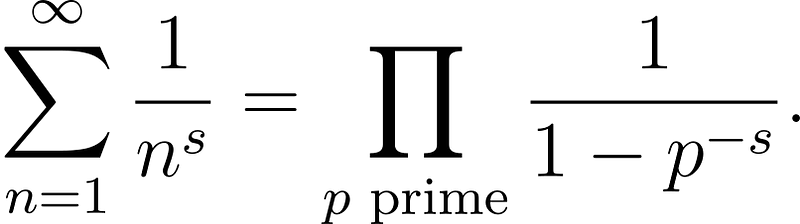
The function defined by either side of the equation for s > 1 is known as the Riemann zeta function, denoted by ζ(s).

Analytic functions like the zeta function have multiple equivalent representations, each defined on different domains. While the expressions above only apply when s > 1, alternative representations may exist for other values, such as s > 0.

It’s important to note that although we primarily consider s as a real number for simplicity, it can also represent complex numbers. The remarkable aspect is that, despite the various forms, there is fundamentally only one function, and all representations coincide regardless of how we extend the function to broader domains. This phenomenon is known as analytic continuation.

Thus, even though ζ(-1) equals the divergent sum of 1 + 2 + 3 + 4 + ..., we can assign a value to this series, and ζ(-1) is the only finite outcome that makes sense.

To evaluate ζ(-1), we must find a representation where ζ is defined at s = -1. Once we find such a representation, we can ascertain that all forms of ζ at s = -1 yield the same value. Various methods can derive this representation, but they consistently result in ζ(-1) = -1/12. This crucial detail was overlooked by the physicists when they derived this value for the divergent series.

Chapter 3: Infinite Products and Regularization

We can also derive finite values instead of infinities by further exploring analytic continuation. For instance, ζ(-2) = 0 and ζ(-3) = 1/120.

These “regularized” values correspond to the infinite series 1 + 4 + 9 + 16 + ... and 1 + 8 + 27 + 64 + ..., respectively. The latter can be utilized to theoretically explain the real phenomenon known as the Casimir force in three dimensions, which serves as a physical testament to the relationship between these values and the infinite series.

So, we can indeed achieve finite values representing infinite sums. That’s fascinating! But what about infinite products? Recall from calculus that d/dx a^x = ln(a) a^x, leading to:

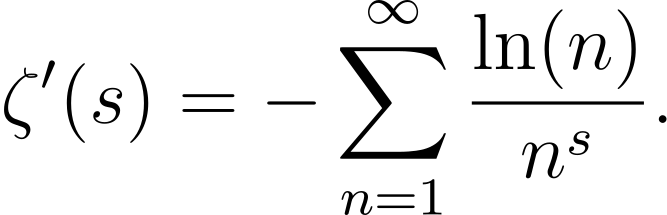
If we seek the regularized product of all natural numbers, we can express it as:

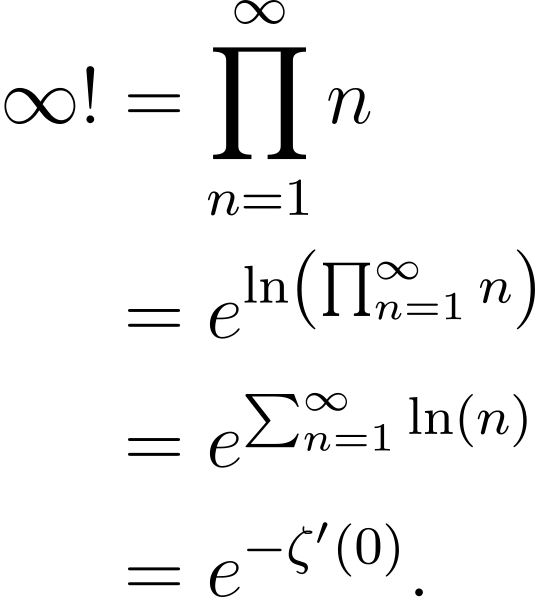
To find a sensible value for the derivative of the zeta function at s=0, we work with an analytic continuation of the series definition above. While proving this value is beyond the scope of this article, I can confirm that ζ´(0) = -1/2 ln(2π).

Armed with this knowledge, we uncover the astonishing result that 1 × 2 × 3 × 4 × ... = (2π)^(1/2) = √2π.

Now, how do we determine the regularized product of the primes?

By manipulating the Euler product over the primes, we can evaluate the expression as follows:

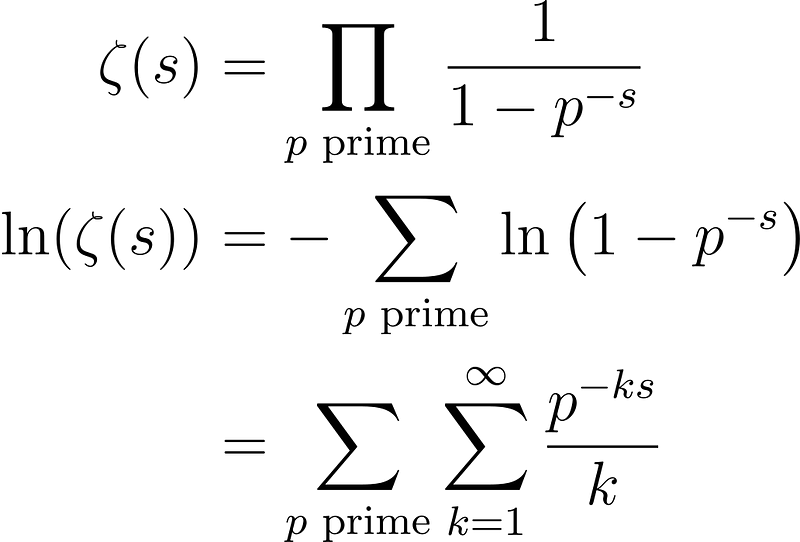
Next, let’s differentiate both sides concerning s:

Note that through regularization and some leniency in notation, we arrive at:

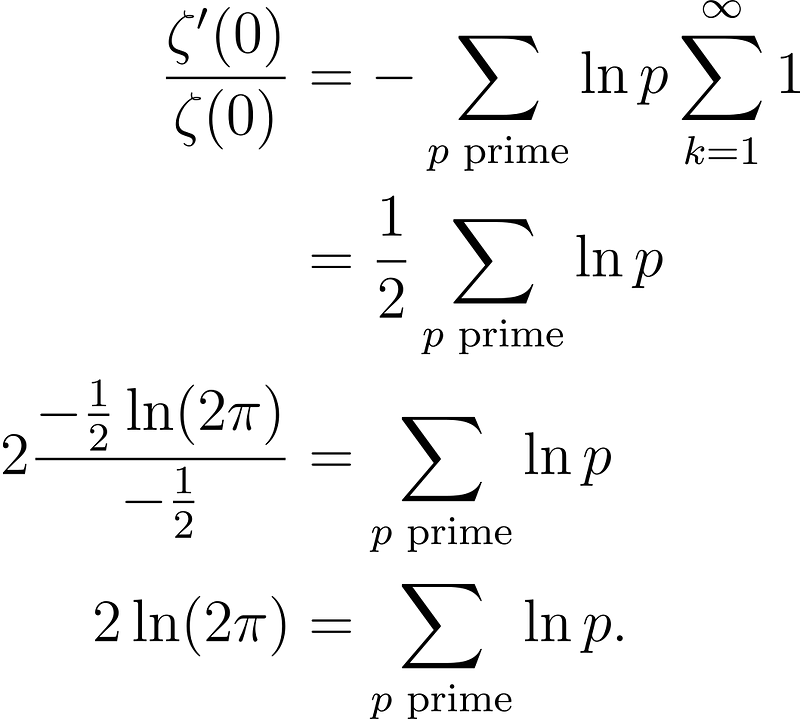
Here, we used that ζ(0) = -1/2. Taking exponentials on both sides yields:

I admit, this proof is rather loose, but there are more rigorous methods that yield the same regularized values. Importantly, these values align with physical experiments and theories.

So, what does this all signify? Is the infinite product of primes genuinely equal to 4²? Ultimately, it hinges on how one interprets the equality sign. In a formal mathematical context, the answer is NO! Yet, a physicist engaged in string theory might assert otherwise.

Regardless, this exploration reveals complexities surrounding infinity that remain elusive, even to me.

Please note that the derivation of the regularized values above is not entirely permissible and serves merely as a heuristic argument. Nevertheless, these values represent the true regularized series and products, with findings such as ζ(-3) = 1/120 emerging in physics as they attempt to sum “infinitely many” energies from standing waves in three-dimensional space.

Chapter 4: Understanding through Visualization

This first video, titled "Amazing Pi Formula - Prime Numbers and Multiples of 4," provides fascinating insights into the connections between prime numbers and pi, offering a visual and conceptual understanding of the topic.

The second video, "Product of Prime Factors," further explores the intriguing notion of prime factors and their products, illustrating the complexities of these mathematical concepts.