The Fascinating Mystery of the Twin Prime Conjecture
Written on
Chapter 1: Understanding Prime Numbers
Prime numbers are fundamental in mathematics, particularly in number theory. By definition, a prime number is one that can only be divided by itself and the number one. For instance, the smallest prime numbers include two, three, and five, while four does not qualify as a prime since it is divisible by two. The significance of prime numbers is underscored by the Fundamental Theorem of Arithmetic, which asserts that every integer greater than one can be expressed uniquely as a product of prime numbers. Thus, prime numbers serve as the building blocks of all integers.
Mathematicians continue to explore the peculiarities of prime number distribution, with a specific focus on twin primes, which present an especially challenging puzzle.
Section 1.1: What Are Twin Primes?
Twin primes are defined simply as pairs of prime numbers that differ by two. The first example of twin primes is the pair consisting of three and five. It's worth noting that the only set of prime numbers that are one unit apart is two and three; this is due to two being the sole even prime number, with all others being odd. Below is a list highlighting the initial pairs of twin primes.

The first eleven pairs of twin primes (Image by Author)
Although many theorems regarding the distribution of prime numbers have been established, twin primes remain a subject of great complexity. In this article, I will discuss some intriguing findings related to twin primes as well as conjectures that remain unproven.
Subsection 1.1.1: Brun’s Theorem
A significant result we have is Brun’s Theorem, which states that the sum of the reciprocals of twin primes converges to a finite value. This theorem, proven by Viggo Brun in 1919, provides critical insights into the distribution of twin primes.
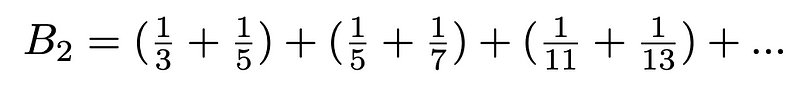
Brun’s Theorem (Image by Author)
The left side of the equation represents Brun’s Constant (B?). Over the years, computers have been employed to calculate Brun’s Constant with increasing accuracy, with the latest estimations placing it at approximately 1.902160583104, based on twin primes below 10¹?. The status of Brun’s Constant as rational or irrational remains an open question, tied to an unproven conjecture discussed later.
The calculation of this constant led to an intriguing, albeit unrelated, discovery. In the early 1990s, mathematician Thomas Nicely, while working on estimates for Brun’s Constant using an Intel Pentium processor, uncovered a significant flaw in the chip that prompted Intel to recall the product. This error reportedly cost Intel around $500 million, an incident now referred to as the Pentium FDIV bug.
Section 1.2: The Twin Prime Conjecture
Brun’s Theorem also suggests the infrequency of twin primes. The calculations indicate that as we move to larger integers, twin primes become increasingly sparse. To simplify this concept, we can define a twin prime function:
??(x) represents the count of primes p ≤ x such that p + 2 is also prime.
Brun’s Theorem allows us to understand the density of twin primes in relation to all prime numbers, revealing that twin primes diminish in frequency at a much faster rate than primes overall. Since the series converges to a constant, it raises the question of whether the number of twin primes is infinite or finite.
The Twin Prime Conjecture posits that there is an infinite number of twin primes. Most mathematicians believe this to be true, although it remains unproven. Given the infinite nature of prime numbers, it seems logical to assume that twin primes would also be infinite. While the infinitude of primes was established over two millennia ago, the twin primes continue to elude definitive proof.
Chapter 2: Progress and Challenges
The quest to prove this conjecture has become a major objective for number theorists. Significant advancements have been made in recent years through innovative methodologies. In 2013, mathematician Yitang Zhang demonstrated that there are infinitely many pairs of primes with a difference less than 70,000,000. This revelation was groundbreaking, especially considering Zhang's relative anonymity at the time, and it marked a notable achievement in the field.

Yitang Zhang (Source)
While a limit of 70,000,000 may not seem particularly remarkable, it represents a crucial step towards proving the Twin Prime Conjecture. The rarity of prime numbers increases as we progress along the number line, potentially leading to greater spacing between them. However, Zhang’s findings indicate a limit on how far apart these primes can be, ensuring that there will always be primes within a specific range of one another.
The next challenge is to reduce this limit all the way down to 2. Through collaborative efforts like the Polymath Project, mathematicians such as Terence Tao and James Maynard, among others, have managed to lower the limit to 246. This remarkable progress could eventually pave the way for a conclusive proof of the Twin Prime Conjecture, and research in this area is ongoing.
The Search for Larger Twin Primes
While discovering larger twin primes does not serve as proof of their infinitude, it remains an engaging pursuit for mathematicians, contributing to our understanding of integers. Numerous online collaborations are dedicated to finding increasingly larger twin primes, with the current record standing at an impressive 388,342 digits. For more information on prime records, including various types of primes, check out The PrimePages.
If you're interested in learning more about twin primes, I recommend the following resources:
- For a discussion on the current state of twin primes and other exciting collaborative mathematical projects, visit the Polymath Blog.
- For an overview of Zhang's proof and insights into the Polymath Project, refer to this article from Quanta Magazine.
- The YouTube channel Numberphile features an engaging video discussing the Twin Prime Conjecture, with contributions from James Maynard, who significantly aided in reducing the gap between primes.
The Twin Prime Conjecture - Numberphile - YouTube
For a well-maintained database of prime numbers and other known primes, The PrimePages is an excellent resource.
I hope you found this exploration enlightening! If you appreciate my work, consider becoming a Medium member to support my writing. You can also follow me for more insights into math and science, as I publish weekly.