Mastering Mental Calculation of Cube Roots for 2-Digit Integers
Written on
Chapter 1: Introduction to Cube Roots
Have you ever wished you could swiftly determine the cube roots of two-digit integers in your head? This fascinating mental math trick can make you appear like a math genius! While cube roots are often regarded as challenging computations not suited for mental calculations, I recently discovered an age-old algorithm that simplifies the process remarkably.
This method allows you to perform these calculations effortlessly, making you look like a math wizard—even if you don’t consider yourself one. I’ve yet to meet anyone who has mastered this technique. Let's dive right into the details!
Section 1.1: Steps to Compute Cube Roots
The first step in this process is the most challenging. However, it’s a one-time effort that pays off significantly. You need to memorize the cubes of the first ten integers, from 1 to 10.
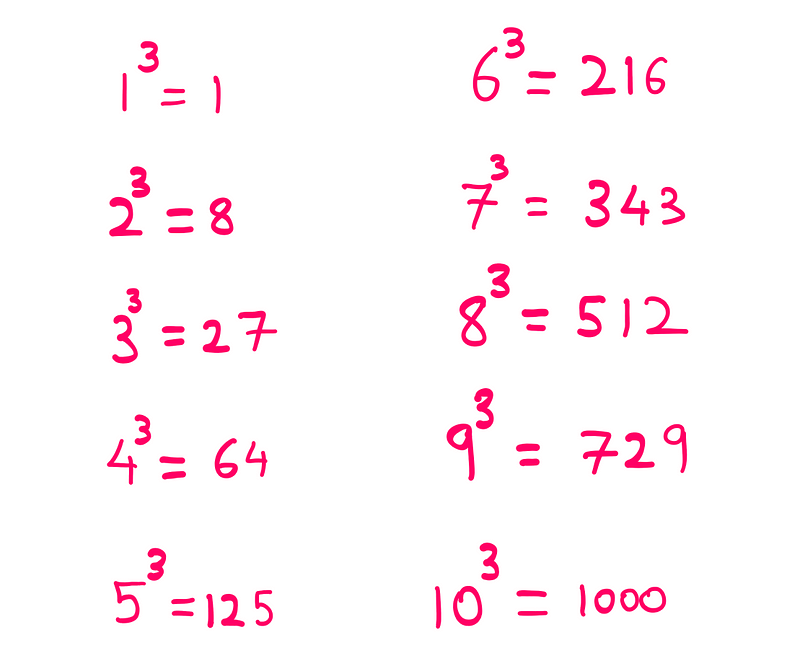
Illustrated by the author
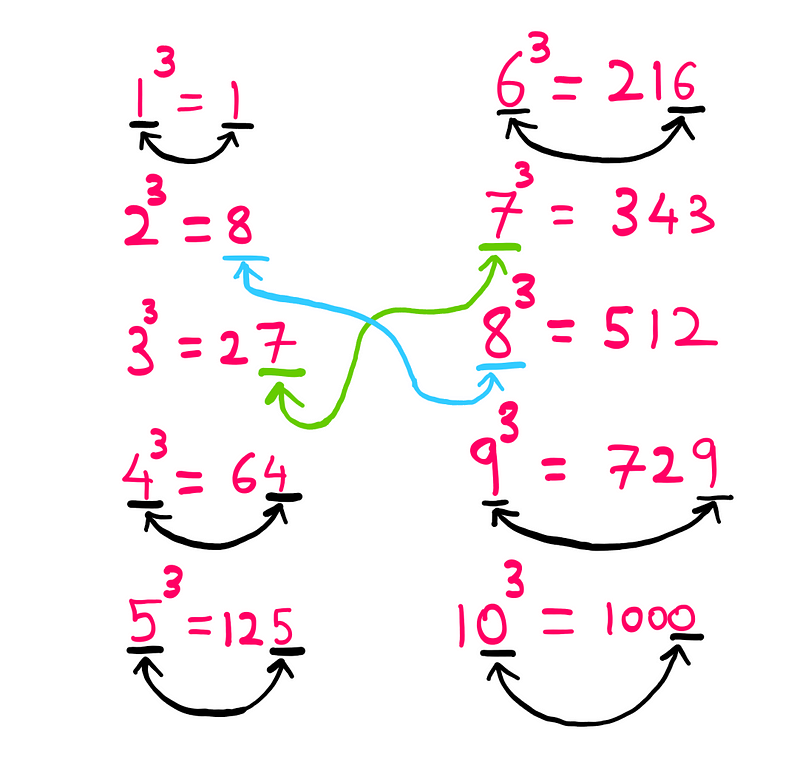
The next crucial aspect of this trick involves recognizing that the ending digits of the cubes correspond to the cubed number for 1, 4, 5, 6, 9, and 10. Additionally, the last digits for the cubes of 2 and 8, as well as 3 and 7, swap places. Once you grasp this concept, you're nearly there!
Illustrated by the author
Subsection 1.1.1: The Final Calculation
Now, let’s consider an example: what is the cube root of 175616? Start by focusing on the last digit, which is ‘6’. From our earlier findings, we know that the cube of 6 also ends in 6.
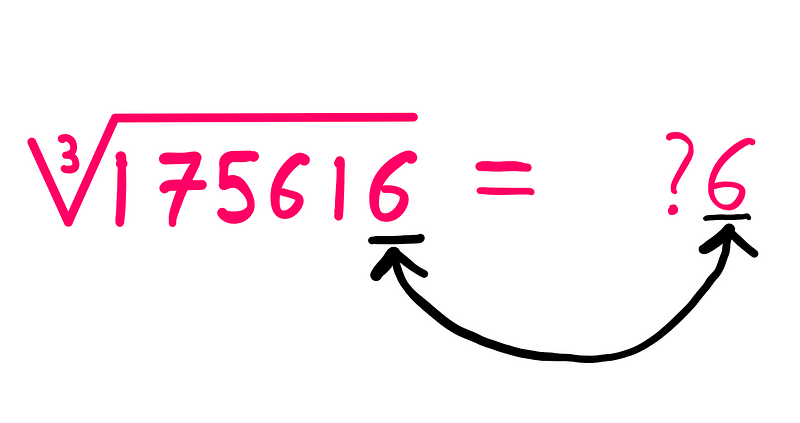
Illustrated by the author
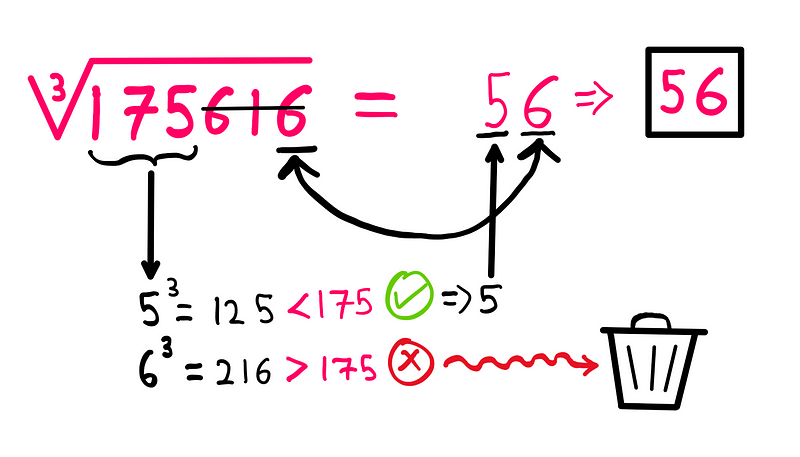
This insight leads us to predict that the cube root of 175616 will end with a 6. Next, disregard the last three digits of 175616 (616) and focus on the first three digits (175). Now, ask yourself, “Which integer between 1 and 10, when cubed, is closest to but not exceeding 175?”
Since 5³ = 125 (less than 175) and 6³ = 216 (greater than 175), the answer is clearly 5. Therefore, placing 5 before 6 gives us the final answer: 56!
Illustrated by the author
Chapter 2: The Mathematics Underlying the Algorithm
At this point, you might be wondering why this method works. Let’s delve into the mathematical principles that underpin this algorithm.
Section 1.2: Understanding the One’s Place
To explain, I will use algebra. Any two-digit integer can be represented in this form:

Illustrated by the author
Now, applying the binomial theorem to cube this expression gives us:

Illustrated by the author
In examining the expansion, it becomes clear that the y³ term will determine the one’s place in the final result. This is why we can confidently ascertain the one’s place digit by merely looking at the last digit of the number for which we are finding the cube root.
For instance, when we consider the number 56, it can be expressed as follows:
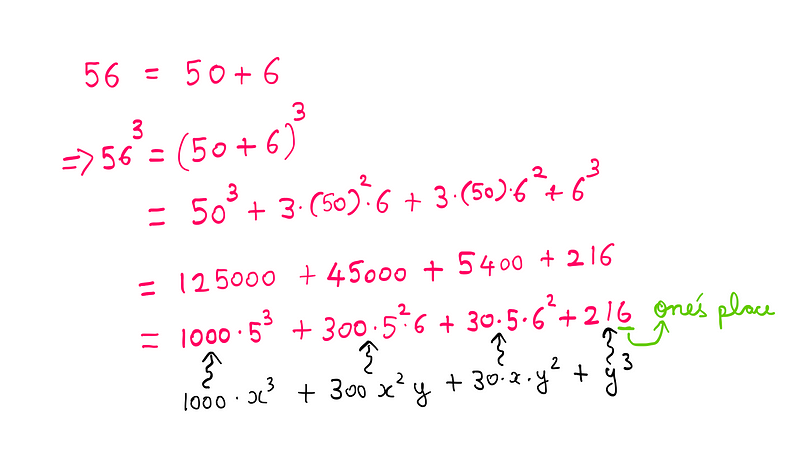
Illustrated by the author
Using standard addition, we find that the sum of the first three terms must end in zero. Consequently, y³ is the only contributor to the one’s place of the cubed number.
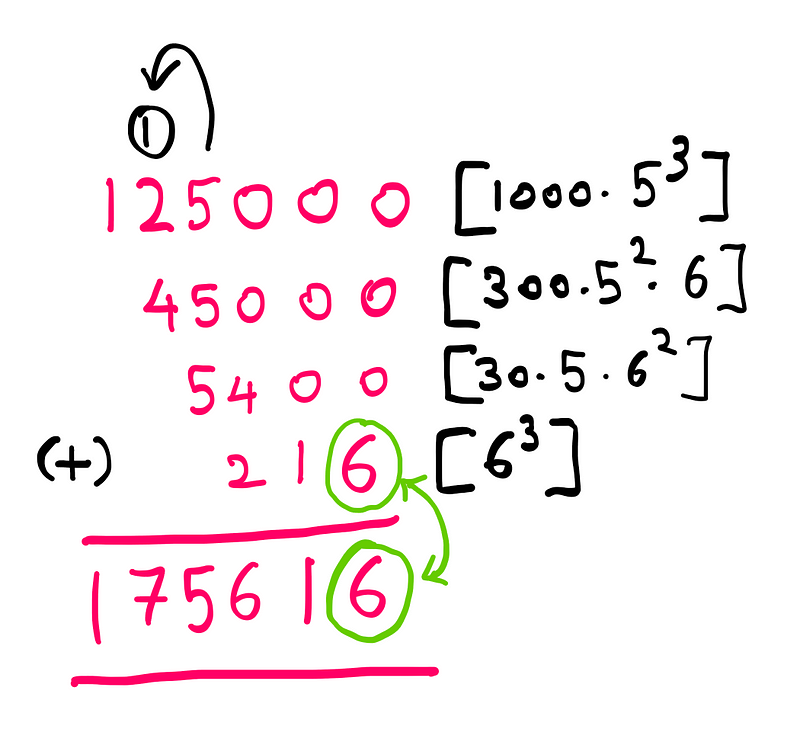
Illustrated by the author
From the last digit of the original number (175616), we’ve identified ‘y’. Now, let’s determine ‘x’.
Section 1.3: Exploring the Ten’s Place
Next, we analyze the first three terms: ‘1000x³ + 300x²y + 30xy²’. The first term (1000*x³) is the primary contributor to the sum and contains only ‘x’.
By dividing the result by 1000, we can concentrate solely on ‘x’, examining the first three digits of the sum (in this case, 175).
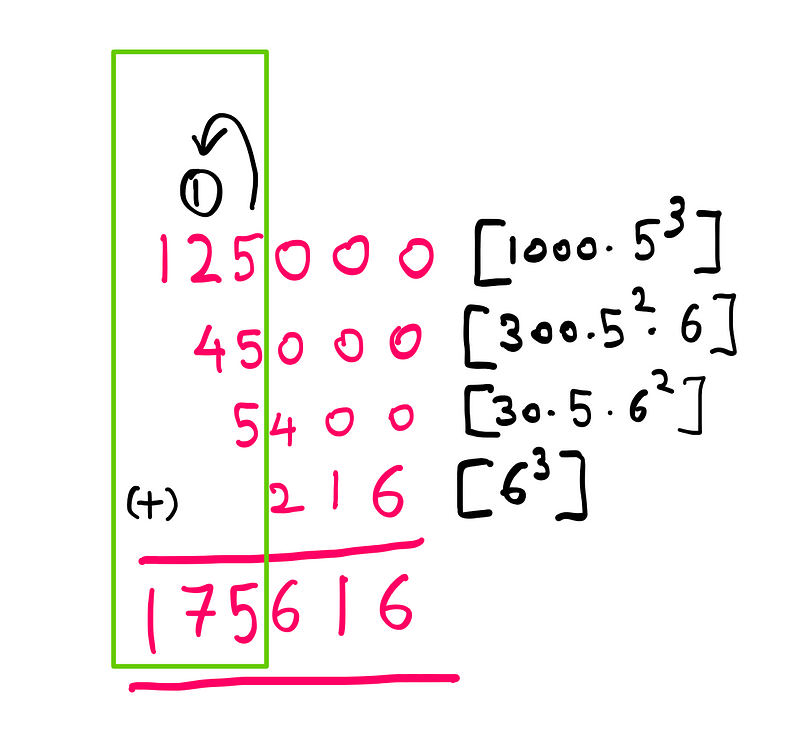
Illustrated by the author
Given the contributions from the terms ‘300x²y + 30xy²’, we know the first three digits must exceed x³. Therefore, we can treat x³ as a lower bound.
To establish an upper bound, we consider ‘(x+1)³’. We can tabulate the expressions ‘[1000x³ + 300x²y + 30xy²]/1000’ and ‘(x+1)³’ against each possible single-digit value of ‘x’ and the maximum value of ‘y’ (which is 9):
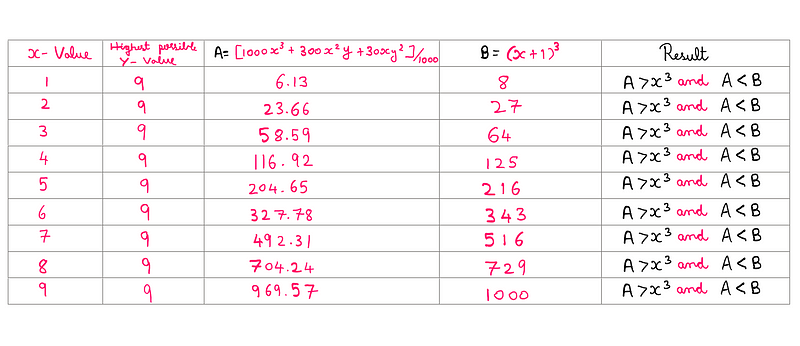
Illustrated by the author
This analysis shows that for the highest ‘y’ value, combined with all potential x values, the expression consistently exceeds x³ yet remains less than (x+1)³. This is why we only need to examine the first three digits of the number (175616) and recall the cube closest to, but not greater than, those three digits.
Chapter 3: Summary and Fun Applications
To summarize the algorithm for mentally calculating cube roots as two-digit integers:
- Memorize the cube values of integers from 1 to 10.
- Recognize that the ending digits of cubes match the cubed numbers for 1, 4, 5, 6, 9, and 10, while the digits swap for pairs 2–8 and 3–7.
- Focus on the last digit of the number for which you're finding the cube root to determine the one’s place.
- Examine the first three digits of that number and recall which cube value is closest to, but not exceeding, those digits.
Now that you’ve mastered this technique, why not have some fun with it? Here’s a suggestion for a party trick:
- Gather a group of math enthusiasts and select someone from the crowd.
- Ask this person to think of a random two-digit integer (without revealing it).
- Request that they cube this integer and share only the final result with you.
- Use your new skills to reveal the original number to the group.
- Enjoy the astonished reactions and wear a smug expression for added drama!
The first video showcases techniques for calculating cube roots in your mind, providing visual aids and a step-by-step guide.
The second video presents a fast math trick for quickly finding the cube root of any number mentally, perfect for impressing your friends!
Reference: Center for Bibliographical Studies and Research (San Francisco Call — 1913).
I hope you found this guide both informative and engaging! If you enjoyed it, consider showing your support by clapping, following, and subscribing for more insights.