Chapter 1: Introduction to Light's Path

In this discussion, my primary focus is to delve into the calculus of variations and leverage the Euler-Lagrange equation for intriguing applications. However, it's essential to begin with simpler problems that demonstrate similar concepts.

To illustrate, I aim to determine the trajectory of light as it transitions from one medium (like air) to another (such as water). This investigation will utilize Fermat's Principle, which posits that light travels along a path that minimizes the time taken. In a homogeneous medium, this would generally equate to the shortest distance, typically a straight line, due to a constant speed. Nevertheless, when light moves between different materials like air and water, its apparent speed is subject to variation.

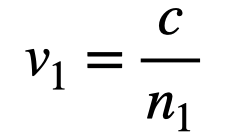
The speed of light is represented as c, while n denotes the index of refraction. When light enters materials with distinct apparent speeds, it must traverse a shorter distance in the slower medium. Consider a scenario where light travels from point A in medium 1 (with index of refraction n1) to point B in another medium (with index of refraction n2). Below is a diagram illustrating this situation.

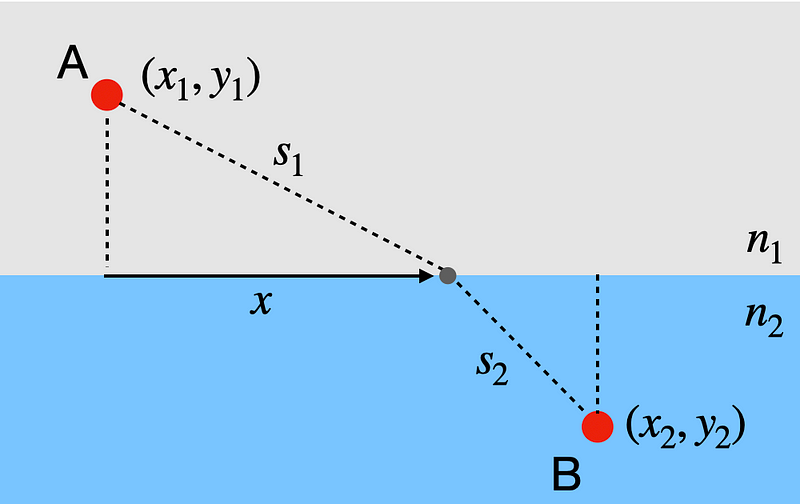
We have various components here, but don't be alarmed; I will clarify each aspect. First, we identify the point on the boundary between the two materials, located a distance of x along the interface from point A's x-coordinate. The light travels in a straight line from A to this point, and then continues in a straight line to B. By adjusting the position of this interface point, I can pinpoint the path that minimizes the travel time. This is the beauty of this problem—while it fundamentally seeks the path of least time (as per calculus of variations), we can frame it as a max-min issue since only one variable (x) is changing.

Once I calculate the path lengths in the two materials (s1 and s2), the total time taken can be expressed as:

However, both s1 and s2 are functions of x (the distance to the interface point). To simplify, I will assume the interface is positioned at y = 0, with point A at x = 0. This makes it easier to derive s1 and s2 as follows:

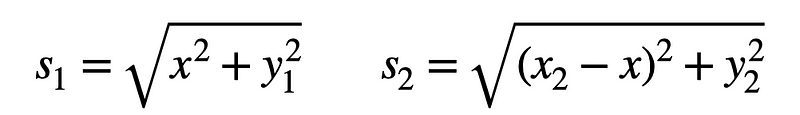
This leads to a total time expression, highlighting a shared denominator of c:

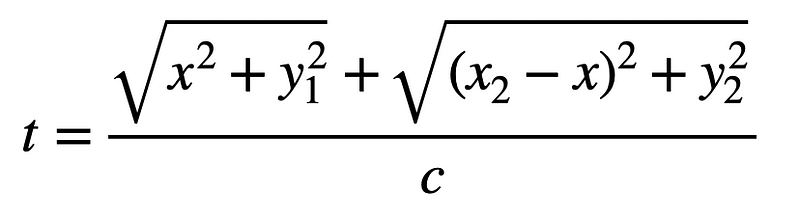
Next, I will differentiate this expression (with respect to x) and set the result to zero to find the optimal value of x. This is a classic max-min problem. To facilitate the differentiation, I'll rewrite the time function.

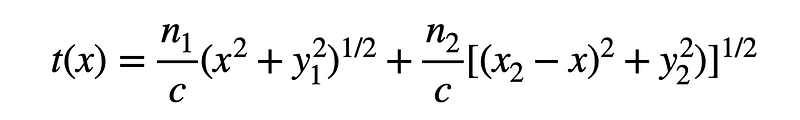
It's important to note that x is the only variable at play. Now, applying the power rule to differentiate:

Setting this derivative to zero and performing some algebra, I arrive at:

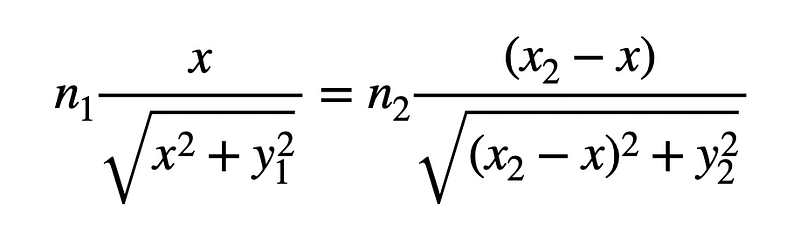
This equation may appear complex, so instead of solving it directly, let’s opt for a different approach. Let’s revisit the diagram for the light's path, this time incorporating angles.

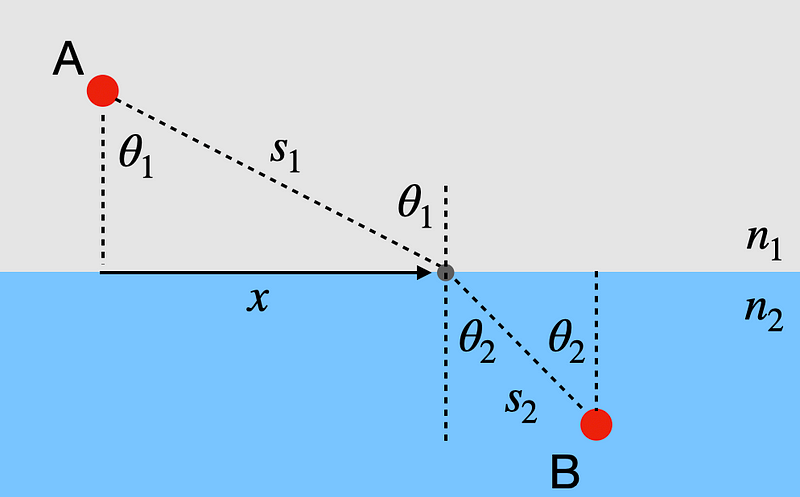
In this scenario, we have two angles, θ1 and θ2. Focusing on θ1 within the right triangle depicted, I can derive expressions for sin(θ1) and sin(θ2) using the known value of s1.

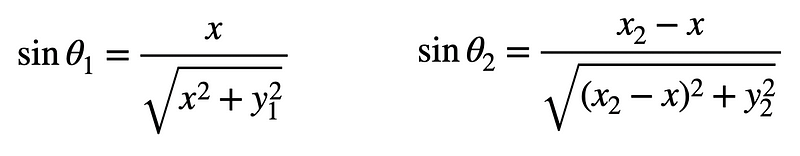
Interestingly, these expressions correspond to the previous equation for the maximum-minimum problem. Substituting these in yields:

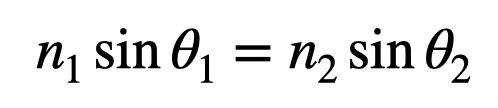
And there you have it! This is Snell’s Law, which establishes a relationship between the indices of refraction and the angles of incidence and refraction of light.

Chapter 2: Further Exploration of Snell's Law

In this chapter, we will further explore the derivation of Snell's Law and its implications.

The first video provides an in-depth look at deriving Snell's Law from Fermat's Principle, framing it as a max-min problem. It’s a valuable resource for visual learners.

The second video covers Max-Min Problems in Calculus 1, specifically detailing how to derive Snell's Law using the principle of least time. This offers a practical approach to understanding the mathematical concepts involved.