Chapter 1: Understanding Trees in Graph Theory

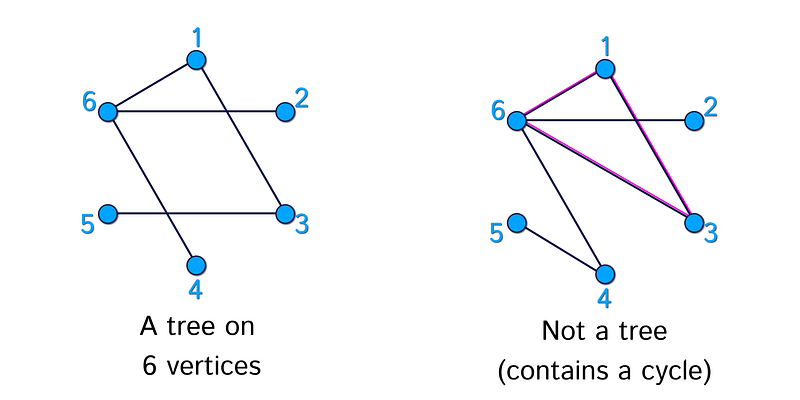
In the realm of graph theory, a tree is defined as a graph that is free from cycles. This concept is fundamental and has numerous practical applications in discrete mathematics.

Trees play a pivotal role in various real-world contexts, from modeling the structure of neurons in the human brain to functioning as decision trees in machine learning and binary search trees in computer science. Additionally, there's the classic family tree that many cherish!

The count of trees that can be formed using n labeled vertices is articulated by Cayley’s Formula, expressed as n^(n - 2). But what is the reasoning behind this formula?

For instance, if we label vertices from 1 to 4, the formula indicates there should be 16 possible trees. This is indeed accurate, as demonstrated in the header image. However, one might wonder why 4 × 4 results in this count. Extending this logic, if we were to label vertices from 1 to 5, would it be logical to conclude there are 5 × 5 × 5 = 125 trees? And for 6 vertices, does it follow that there are 6 × 6 × 6 × 6 = 1296 trees?

Let’s delve into the case of 6 vertices and explore the origin of 6 × 6 × 6 × 6. This suggests we have 6 choices for 4 sequential selections. But what are these 4 selections, and why are there 6 of them?

This is where the Prüfer sequence comes into play, shedding light on the clever encoding of trees.

The Beauty of Graph Theory: Trees and Their Applications

A Prüfer sequence is a smart mechanism to represent any tree with n vertices as a sequence of length (n - 2), where each element can be any number from 1 to n. Below are some examples of Prüfer sequences and their corresponding trees.

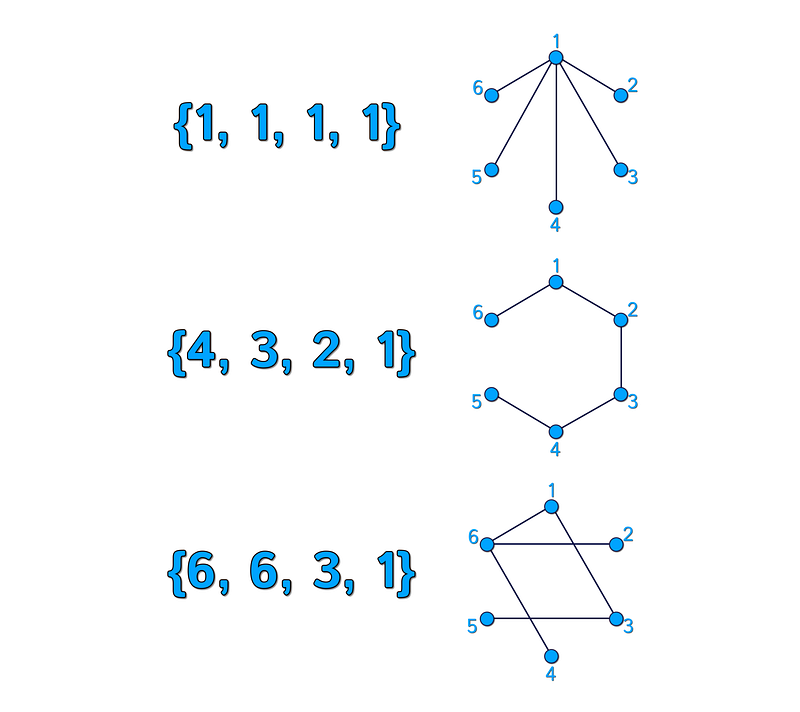
Since each number can be any value from 1 to n, the total number of Prüfer sequences of length (n - 2) amounts to n^(n - 2).

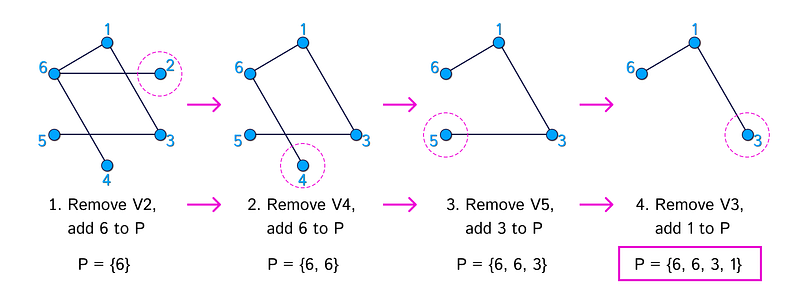
Now, let's demonstrate why each tree corresponds to a unique Prüfer sequence, and vice versa. We will utilize the third example, featuring the Prüfer sequence {6, 6, 3, 1}. The creation of a Prüfer sequence from a given tree is surprisingly straightforward: simply remove the leaves of the tree in ascending order. A leaf is defined as a vertex with a degree of 1.

More formally, the process is as follows:

By continuing until the tree's degree reaches 2, this algorithm necessitates (n - 2) iterations and produces a list of (n - 2) numbers. The diagram below illustrates the four iterations required to derive the Prüfer sequence {6, 6, 3, 1} from its associated tree.

To confirm that the Prüfer sequence generated for each tree is distinct, we observe that there is only one selection at each step. Specifically, the vertex with a degree of 1 and the lowest label is unique. Moreover, the neighbor of this vertex is also unique due to its degree being 1.

This uniqueness implies that the function mapping trees to Prüfer sequences is injective, meaning no two trees can yield the same Prüfer sequence. To demonstrate that the number of Prüfer sequences matches the number of labeled trees, we must further establish that this function is bijective. This entails showing that each Prüfer sequence corresponds to a distinct tree.

The method to reconstruct a tree from a Prüfer sequence effectively reverses the earlier process, albeit it appears more complex as we are tasked with generating a tree rather than a simple number list.

The subsequent diagram presents the five steps needed to derive the unique tree linked with the Prüfer sequence {6, 6, 3, 1}.

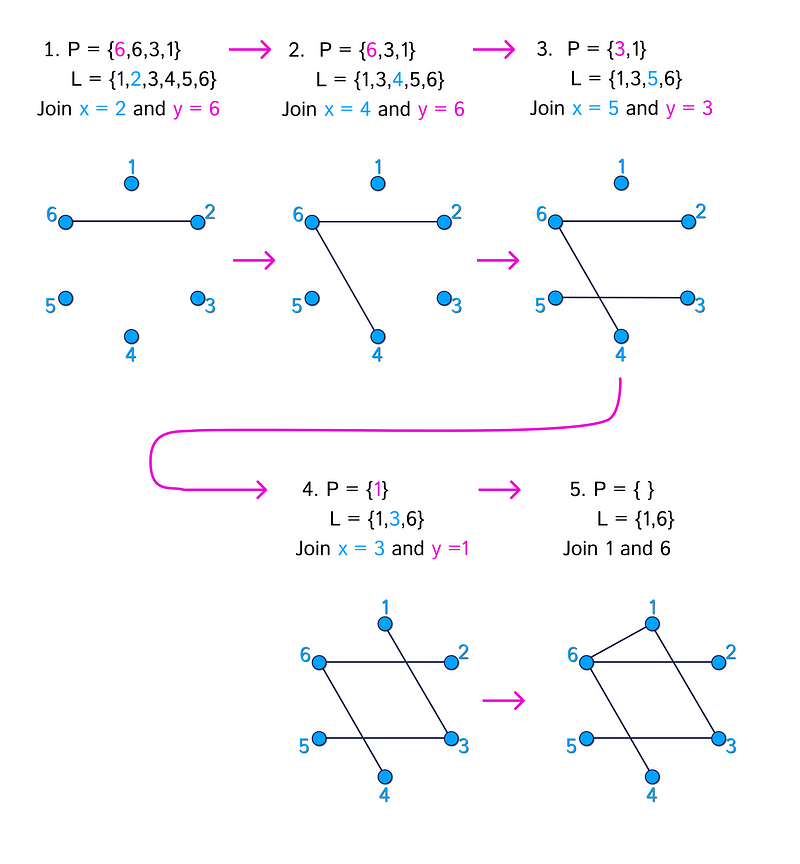
For an additional example, observe the diagram depicting the five steps to obtain the unique tree related to the Prüfer sequence {4, 3, 2, 1}.

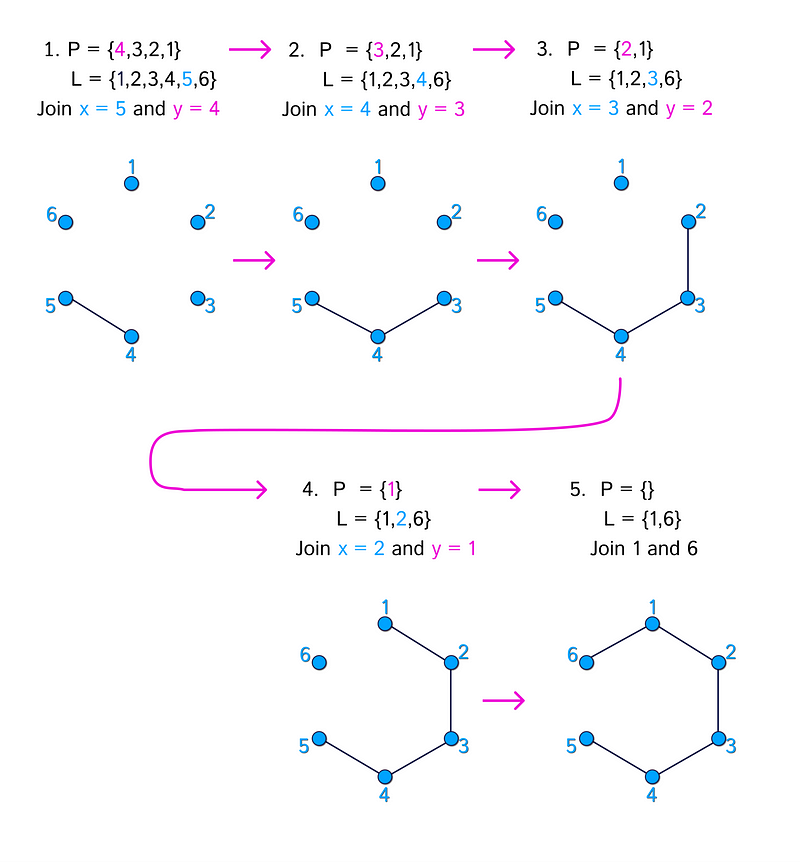
Examining the algorithm again confirms that at every stage, there is a singular option available. There must exist a unique x, the smallest label in L, and a unique y, the first label in P.

This establishes that each Prüfer sequence corresponds to a unique tree, thereby proving that the mapping between labeled trees and Prüfer sequences is indeed bijective. Consequently, the number of Prüfer sequences equals the number of labeled trees, resulting in n^(n - 2).

As for how Heinz Prüfer conceived this elegant and ingenious algorithm back in 1918, that remains an intriguing mystery! If you have any insights into the thought process behind it, please feel free to share your thoughts.

Daniel Spielman: Miracles of Algebraic Graph Theory