Chapter 1: The Legacy of Marin Mersenne

In this brief overview, we embark on an intriguing exploration of prime numbers and their historical significance. Our journey begins in France with the remarkable life of Marin Mersenne, who was born on September 8, 1588. Renowned as a priest, mathematician, and scientist, Mersenne's curiosity spanned various subjects, from the physics of vibrating strings to diverse mathematical concepts.

Mersenne was a central figure in the scientific community of his era, engaging in correspondence with luminaries such as Galileo Galilei, René Descartes, Étienne Pascal, and Pierre de Fermat. Although he was not solely a mathematician, his name is forever associated with Mersenne primes—a specific category of prime numbers that he famously cataloged. Though these primes had been examined nearly 2000 years prior to his birth, Mersenne's compilations gained widespread recognition.

Throughout history, mathematicians endeavored to validate the primality of the numbers Mersenne listed—some of which were not prime. This monumental task was complicated by the sheer size of these numbers. For example, Mersenne asserted that 2¹²? - 1 is a prime number, a claim validated by Édouard Lucas in 1876. Remarkably, this was the largest prime number discovered through manual calculation up until that point.

Perfect Numbers and Mersenne Primes

The connection between perfect numbers and Mersenne primes will be further discussed in the upcoming sections.

Section 1.1: Understanding Mersenne Numbers

To delve deeper, let's define what constitutes a Mersenne prime. Not every number that fits the Mersenne formula is prime, yet the following holds true:

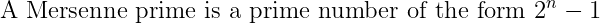
The theorem can be proven through its contrapositive:

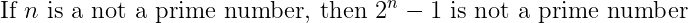
Proof Overview:

Assuming n is a composite number, we can express it as n = ab, where a and b are greater than 1. Utilizing the closed form of the power sum, we can demonstrate the theorem's validity:

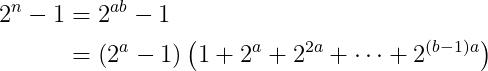
A number of this form, whether prime or not, is referred to as a Mersenne number. It's essential to note that not all Mersenne numbers with prime exponents are prime themselves; for example, 2¹¹ - 1 equals 23 × 89, which is composite. This insight leads to the conclusion that searching for large primes can be optimized by focusing on Mersenne numbers with prime exponents—a strategy that proves effective as Mersenne primes become increasingly rare with larger exponents.

Chapter 2: The Ongoing Quest for Primes

Despite Mersenne leaving no records detailing the origins of the numbers he listed, the quest for prime numbers continues unabated. Presently, the largest known primes are Mersenne primes, which play a vital role in cybersecurity and cryptography. Many algorithms, such as RSA, are heavily reliant on prime numbers, underscoring their relevance in contemporary society—a notion Mersenne likely never envisioned.

Mersenne's initial list has been expanded significantly thanks to modern computing. However, the question of whether an infinite number of Mersenne primes exists remains unresolved—a problem that has baffled mathematicians including Euler and still lacks a definitive answer today.

The Connection with Perfect Numbers

In conclusion, we will explore the intriguing relationship between Mersenne primes and perfect numbers in the next article. Until then, happy exploring!