Understanding Infinite Nested Fraction Integrals Simplified
Written on
Chapter 1: Introduction to Nested Fractions
Have you ever wondered how to simplify an infinite nested fraction? This article delves into the process and provides a step-by-step solution.
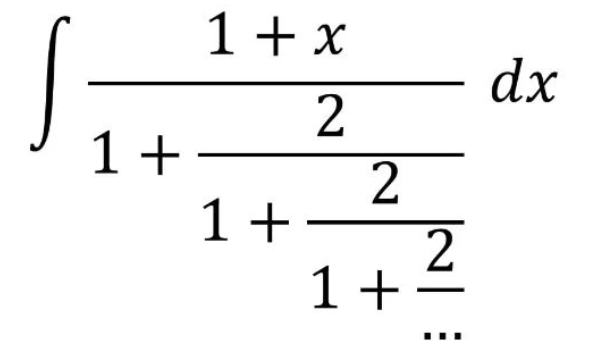
If all components being added are positive, the result cannot be negative. This insight serves as a crucial hint for solving the problem. I suggest you pause here, attempt to solve it on your own, and resume reading when you’re prepared for the solution.
Section 1.1: Breaking Down the Expression
The expression may appear complex at first glance, but we can simplify it by letting the denominator equal (y).
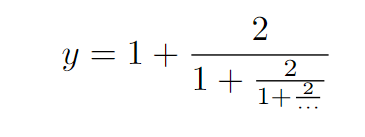
Since the dotted section of the expression continues indefinitely, it also equates to (y).
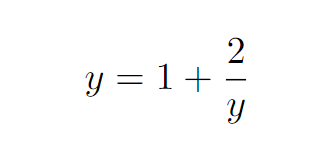
A special thanks to Aaron Horak for highlighting the earlier mistake. This leads us to a quadratic equation.
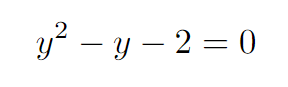
Typically, this equation would yield two solutions: (y = 2) and (y = -1). However, since (y) must converge to a positive value, we conclude that (y) is equal to 2. Consequently, we need to evaluate the following.
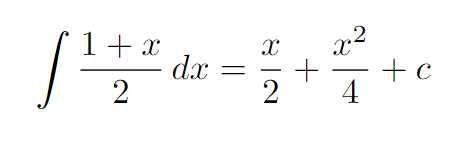
Don't forget to include the constant of integration in your final answer! That concludes our solution. Did you arrive at the same conclusion? What was your method? I'm curious to hear your thoughts in the comments below!
The first video, "A logarithmic continued fraction integral," provides a deeper understanding of the concepts discussed here.
Section 1.2: Engaging with Math Puzzles
If you enjoyed this exploration of nested fractions, consider sharing these intriguing math puzzles available on Medium. They span various topics including Algebra, Geometry, Calculus, and Number Theory.
The second video, "Infinite Continued Fractions, simple or not?" further challenges our understanding of these mathematical principles.
Chapter 2: Conclusion and Community Engagement
Thank you for taking the time to read this article! If you found it insightful, please consider supporting my work. Your encouragement means the world to me.

I appreciate all the time and effort invested in writing for you. If you're feeling generous, a coffee would be a wonderful way to support my writing journey. Thank you for your kindness!