Chapter 1: The Concept of Jumping High

Currently, I am delving into Randall Munroe's book, How To (Penguin Random House), and I must say, I have a great appreciation for his work, particularly his engaging xkcd comics.

The premise of this book is to tackle both bizarre and ordinary questions, providing guidance on how to achieve them. One intriguing question posed is: "How can one jump higher?" Naturally, being a book, it glosses over some intricate details, which is where I come in. My goal is to illuminate the missing elements of the equations he presents.

To start, let’s consider how speed can be transformed into upward velocity, allowing you to propel yourself into the air. This scenario is akin to riding a skateboard and encountering a vertical ramp. Munroe presents the following equation, which I've recreated using LaTeX.

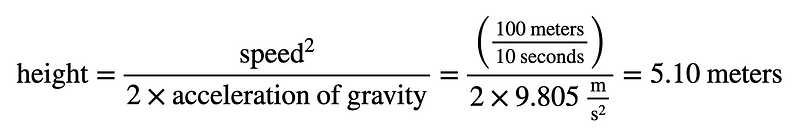
Indeed, replicating this was a bit of a challenge. I utilized Apple Keynote, which has its own way of handling LaTeX. Here’s the equation:

[

mathrm{height}=frac{mathrm{speed}^2}{2 times mathrm{acceleration}medspace mathrm{of}medspace mathrm{gravity}}=frac{left(frac{100 medspace mathrm{meters}}{10 medspace mathrm{seconds}}right)}{2 times 9.805 medspace frac{mathrm{m}}{mathrm{s}^2}}=5.10 medspace mathrm{meters}

]

You don't need to worry about the LaTeX code; I just wanted to demonstrate my ability to recreate the equation.

Before we dive deeper into the derivation of this equation, I have a few observations:

1. There’s an error in his calculation; he omitted the “squared” part when discussing velocity.
2. The equation is presented in metric units—definitely a plus!
3. The term “acceleration of gravity” doesn’t sit well with me. A simpler term, such as “g” or “gravitational field,” would be preferable. Commonly, it’s referred to as “acceleration DUE TO gravity,” which I still find unsatisfactory.
4. While using speed instead of velocity is acceptable, it can lead to confusion.

Let’s proceed with the derivation.

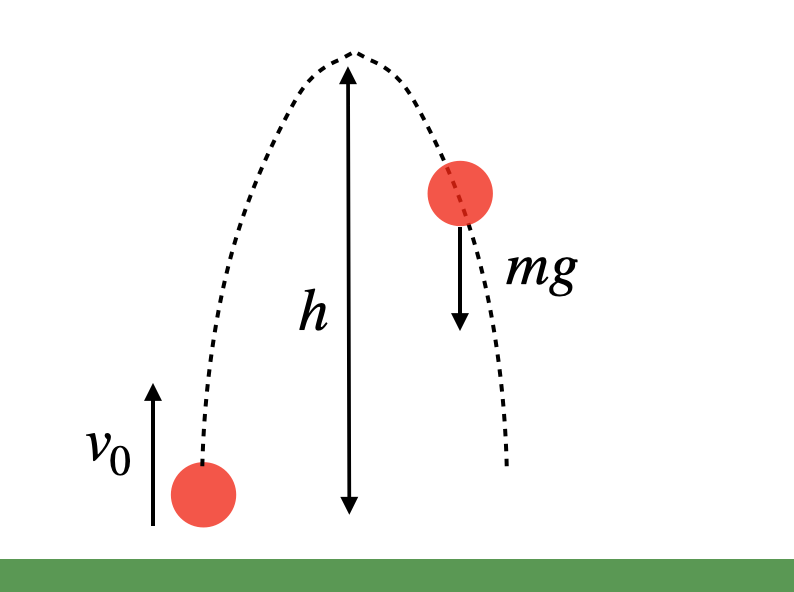
Imagine tossing a ball straight up with an initial velocity. Upon release, only one major force acts upon it: gravity, which pulls it downward. The strength of this gravitational force is contingent on the object's mass (m) and the gravitational field strength (g).

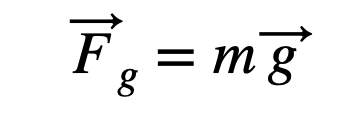
Both the gravitational force and the gravitational field are vector quantities. As the product of mass and gravitational field strength (m*g) must be expressed in Newtons, the magnitude of the gravitational field is defined as:

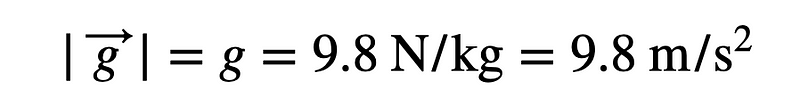
Just a couple of notes:

• Since g denotes the gravitational field's magnitude, it should be treated as positive. Avoid writing g = -9.8 N/kg as it may reflect poorly on your physics knowledge.
• Remember that a Newton is defined as kg*m/s², so dividing a Newton by a kilogram yields m/s², the unit for acceleration.

The net force acting on the ball is m*g, and according to Newton's second law (considering only the vertical direction):

Consequently, the ball experiences an acceleration of -9.8 m/s². If it starts with a positive initial velocity (v0) and this acceleration of -g, how high can it ascend? While kinematic equations could provide an answer, I prefer to begin with the fundamental concepts of acceleration and average velocity.

To clarify, let’s define acceleration.

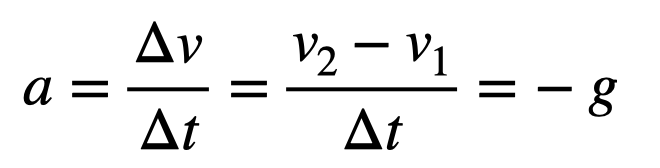
Acceleration, being the rate of change of velocity, is expressed as the change in velocity (final velocity v2 minus initial velocity v1) divided by the time taken. Given that this acceleration is -g, it implies the change in velocity is directed downward. If the ball ascends (positive y-velocity), it decelerates. Conversely, if it's descending (negative velocity), it accelerates.

However, this acceleration equation does not provide the maximum height. To ascertain this, we recognize that when the ball reaches its peak, it transitions from upward (positive velocity) to downward (negative velocity), meaning it must pass through zero velocity.

This allows us to calculate the time taken to reach the apex.

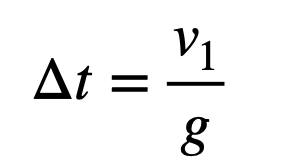
Note: This expression is valid only when the final velocity equals zero, and it indeed yields a positive time interval, which is encouraging.

Now, let’s shift our focus to the average velocity definition.

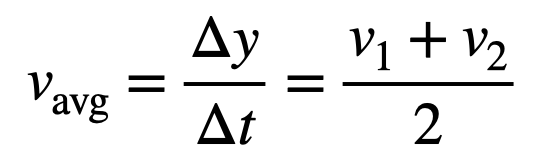
There are two interpretations of average velocity: it represents the change in position over time, and it can also be calculated as the mean of initial and final velocities. This presumes that the velocity alters at a constant rate (constant acceleration).

I aim to determine the change in position (?y), which corresponds to the total height of the ball (or jumper). At the highest point, v2 remains zero. By employing both definitions of average velocity, we can solve for the change in position.

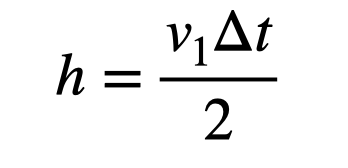
Next, substituting my expression for the time interval yields:

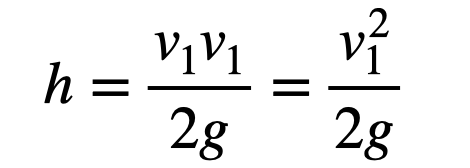
And voila! This matches the equation derived in How To.

What about calculating the actual height? No worries—I'll provide a Python script for that. Here’s the code, along with its output.

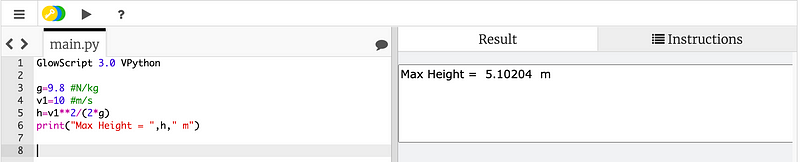
That sums up the jumping equation presented in How To.

Chapter 2: Video Insights on Jumping Mechanics

In this fascinating video, Randall Munroe explores whether it's feasible to alter the color of the moon, highlighting the intersection of creativity and physics.

This video presents a humorous take on using tennis balls to hit drones, showcasing a playful approach to physics and technology.