Calculating Mars' Diameter Using Small-Angle Approximations
Written on
Chapter 1: Introduction to Small-Angle Approximations
Small-angle approximations involve the assumption that for very small angles θ, the sine and cosine functions can be simplified. This is particularly useful in calculations involving celestial bodies. For instance, on August 27, 2003, Mars approached Earth more closely than ever recorded. This event presents an opportunity to apply these approximations to estimate the diameter of the red planet.
Before diving deeper, let's revisit some foundational concepts: what are sin θ, cos θ, and tan θ? These functions are typically understood through the context of right triangles.
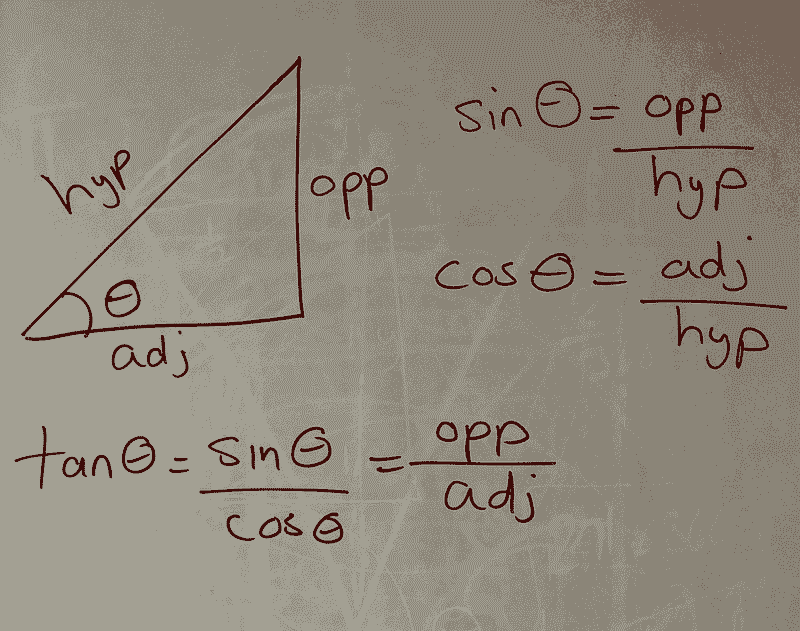
Section 1.1: Understanding Radians
While angles are often expressed in degrees—like the four 90-degree angles in a square—using radians can be more practical. For example, in a circle with radius r, if two lines are drawn from the center creating an angle θ, then θ equals 1 radian when the arc length equals r.
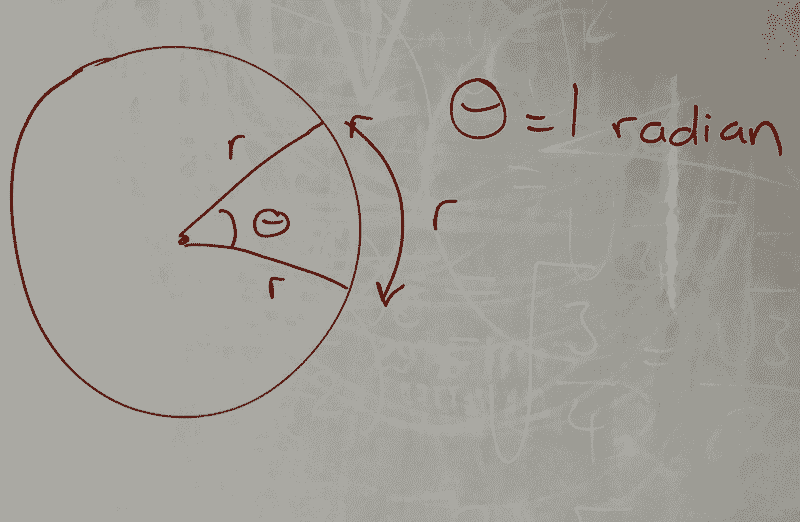
Given that the circumference of a circle is 2πr, it follows that 360 degrees corresponds to 2π radians. Therefore, 1 radian equals approximately 57.2958 degrees.
How is arc length determined? The arc length for any angle θ in radians is given by the formula: arc length = rθ.
For instance, if θ equals 1 radian, the length is r, and if θ equals 2π radians, it results in the circumference, 2πr.
Section 1.2: Sine and Cosine in Small Angles
Consider a circle with a radius of 1 unit positioned on the xy-plane, where θ is the angle formed with the x-axis.
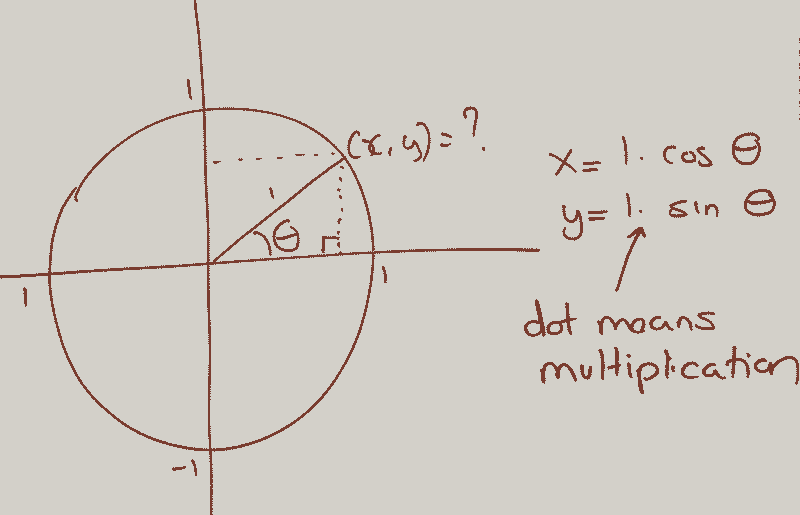
At the intersection point with the circle, the values of x and y can be expressed as follows: y = 1 * sin(θ) = sin(θ) and x = 1 * cos(θ) = cos(θ). The distance along the arc from the point (1,0) to the intersection is simply 1 * θ, according to our arc length formula.
As the angle θ diminishes, the arc length and the vertical height (y) converge, implying that sin(θ) approaches θ. Similarly, as θ approaches zero, the hypotenuse and the adjacent side nearly equal each other, indicating that cos(θ) approaches 1.
To visualize this further, we can look at the graphs of y = sin(θ), y = cos(θ), and y = θ.
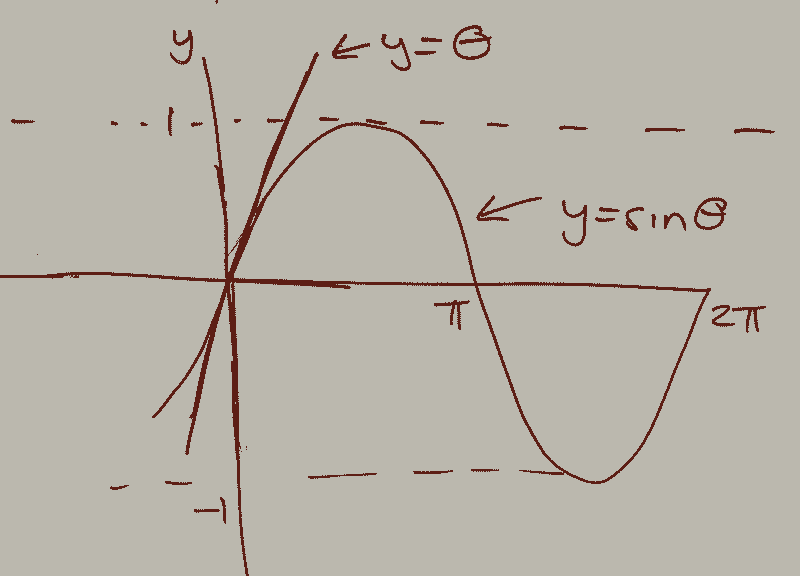
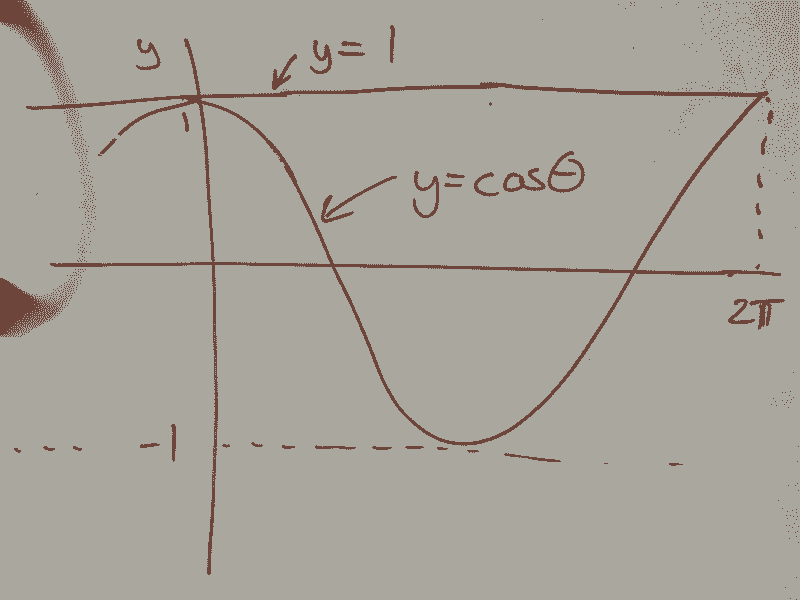
At the points (0,0) and (0,1), we observe that both sin(θ) and cos(θ) approximate their linear counterparts for very small θ. The derivative at (0,0) for both functions equals 1, while at (0,1), the derivative for cos(θ) equals 0, indicating that cos(θ) resembles the line y=1 for small angles.
Chapter 2: Practical Calculations
To verify our understanding, let's calculate some values:
- sin(1 radian) = 0.8414
- sin(0.5 radians) = 0.4794
- sin(0.25 radians) = 0.2474
- sin(0.1 radians) = 0.0998
- sin(0.01 radians) = 0.0099
- cos(1 radian) = 0.5403
- cos(0.5 radians) = 0.8775
- cos(0.25 radians) = 0.9689
- cos(0.1 radians) = 0.9950
- cos(0.01 radians) = 0.9999
The first video titled "Small Angle Approximations" provides an insightful overview of how these approximations work in various contexts.
Diameter of Mars
Now, returning to our initial problem: on August 27, 2003, Mars was at its closest point to Earth, roughly 55.8 million km away. The angular diameter of Mars was measured at about 25.1 arcseconds.
What does angular diameter mean? It refers to the angle formed by two lines that extend from the observer to the opposite ends of Mars.
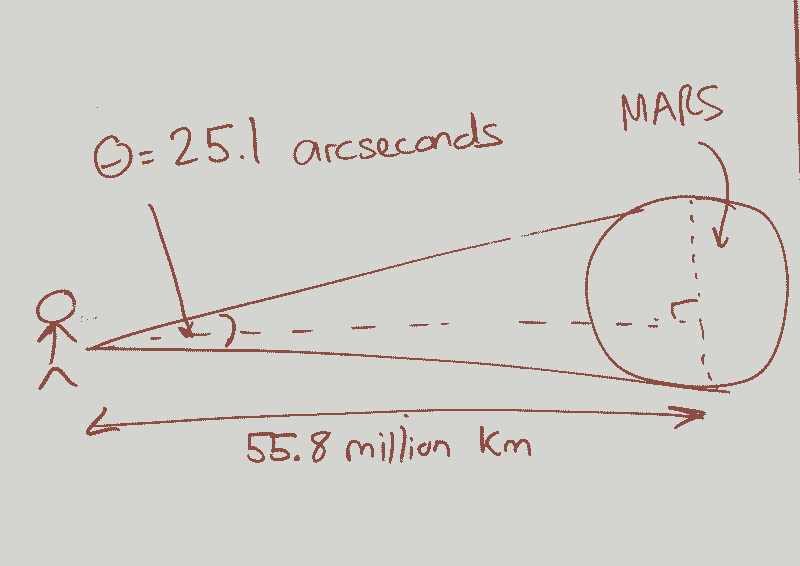
To clarify, an arcsecond is a small angle measurement: 1 arcsecond is 1/3600 of a degree, making 3600 arcseconds equal to 1 degree. One radian translates to approximately 206264.8 arcseconds.
Using the right triangle model, we can find Mars' radius, where the adjacent length is 55.8 million km, and the angle is half of 25.1 arcseconds converted to radians (12.55 arcseconds = 0.00006084411 radians).
Applying our small-angle approximations, we have sin(0.00006084411) ≈ 0.00006084411 and cos(0.00006084411) ≈ 1. Thus, the tangent can be expressed as tan(0.00006084411) = 0.00006084411.
Calculating the radius of Mars, we find 0.00006084411 multiplied by 55.8 million km results in a radius of approximately 3395.10 km. Consequently, the diameter is about 6790.2 km (doubling the radius).
According to Google, the established diameter of Mars is 6779 km, revealing a remarkably close approximation on our part, within just 11 km!

I'm eager to explore more applications of small-angle approximations. Feel free to share your thoughts or ideas in the comments below.
The second video titled "Small Angle Approximations (1 of 4: Proof)" delves into the theoretical aspects and proofs surrounding these mathematical principles.